Alternatization
In mathematics, the notion of alternatization or alternatisation is used to pass from any map to an alternating map.
Let  be a set and
be a set and  an Abelian group. Given a map
an Abelian group. Given a map 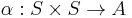 ,
,  is termed an alternating map if
is termed an alternating map if 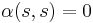 for all
for all 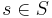 and
and 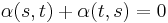 for all
for all 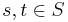 .
.
The alternatization of a general (not necessarily alternating) map 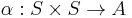 is the map
is the map 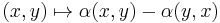 .
.
The alternatization of an alternating map is simply its double, while the alternatization of a symmetric map is zero.
The alternatization of a bilinear map is bilinear. There may be non-bilinear maps whose alternatization is also bilinear. Most notably, the alternatization of any cocycle is bilinear. This fact plays a crucial role in identifying the second cohomology group of a lattice with the group of alternating bilinear forms on a lattice.